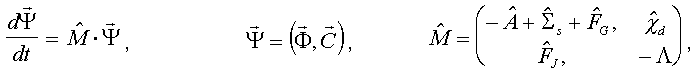
In Proceedings of INFORUM-99 Annual Meeting on Nuclear Technology, 19-23 (Karlsruhe, Germany, 18-20 May 1999).
DEVELOPMENT
OF EXPLICIT CYCLIC SCHEMES
WITH CHEBYSHEV’S POLYNOMIALS FOR SPACE NEUTRON KINETICS
ON THE MULTIPROCESSOR COMPUTERS
V. Arzhanov, A. Voronkov, A. Golubev, E. Zemskov, N. Konovalov, V. Krukov
Keldysh
Institute of Applied Mathematics, Russian Academy of Sciences
(KIAM RAS)
Questions have been studied to use effectively explicit schemes for solving spatial kinetics. These schemes use multi-step computational cycles with parameters determined by Chebyshev’s polynomials. The spatial kinetics problem is considered in the general evolution form. Analytical expressions have been derived for step operators from one time level to the next one as applied to the cyclic schemes.
Algorithms have been developed to solve spatial kinetic equations on the basis of explicit cyclic schemes with time varying steps designed by V.I. Lebedev [1] as well as schemes of local iterations proposed by O.V. Lokutsievskiy and V.O. Lokutsievskiy [2].
The system of equations for description of the space neutron kinetics in nuclear reactors may be written in the following operational form:
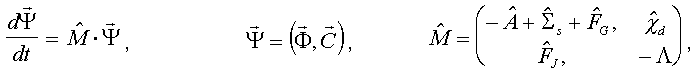
where:
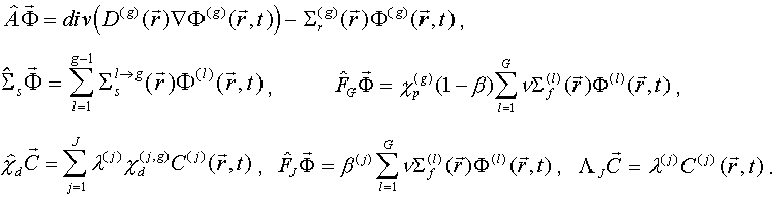
We consider that 
is the solution on
time step number n. We need to
find the solution on n+1 time
step. Let time step 
is chosen for given precision, 
, where 
is the
time step of explicit scheme and 
is the maximum
eigenvalue of matrix M at tn. We can implement cycle of p - iteration, which depends from condition of
stability cycle [3]:
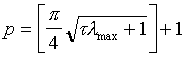
(the square brackets mean the integer part of number). Full cycle is described by the following algorithm:
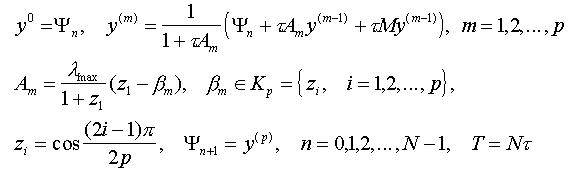
where Kp - the set of the Chebyshev’s polynomial roots for p - degree with special ranking [4]. Factor A1 = 0, therefore first iteration is equivalent to the explicit scheme.
A sequential version of the code for implementation of above written schemes was developed in Fortran-77 language. The experience of development of the parallel version of this code in Fortran-77 language with MPI library confirms the well-known opinion: the message passing approach has essential shortcomings.
First, the level of language facilities supporting program parallelism is too low. The lack of the global address and name space requires serious efforts for writing parallel programs. The debugging of message passing programs is still an open problem and a serious disadvantage for industrial development of parallel codes.
Second, the efficient program execution on massively parallel computers requires load balancing which is extremely difficult to provide in the message passing model.
It is necessary to develop new methods and tools for creating portable and efficient parallel programs for distributed memory computers.
The data parallel language Fortran-DVM was developed in KIAM on the basis of the DVM-model [5, 6]. The DVM name originates from two main notions - Distributed Virtual Memory and Distributed Virtual Machine. The former reflects the global address space, and the latter reflects the use of an intermediate abstract machine for the two-step mapping of the parallel program onto a real parallel computer.
The parallel program in Fortran-DVM is a code in the standard Fortran-77 language, in which the DVM directives (annotations) specifying parallel execution of the program are inserted. The directives are transparent for standard Fortran-77 compilers, therefore DVM programs can be executed on workstations as usual sequential programs.
Therefore the new version of parallel code was implemented in Fortran-DVM language.The experience on developing program in the Fortran-DVM language allows us to state that the Fortran-DVM programming system makes it much easier to develop the effective and portability programs on parallel computers.
To verify the developed numerical methods and codes in Fortran-DVM for thermal nuclear reactors (REACP program package) the three-dimensional hexagonal dynamic AER Benchmark problem A [7] is used.
In Benchmark A the transient processes were caused by ejection of an asymmetric control rod in a VVER-core with zero power for 0.08 second. Feed back effects were neglected. One second later the shut down rods are inserted in core to suppress slow power increase. The purpose of Benchmark A is to determine the calculation precision of the transient process taking into account delayed neutrons. Our numerical results were compared with the results calculated by DYN3D code [8] and READYN code [9]. In calculations 24 points for axial direction Z and six points per each hexagon are used. In Fig. 1 there is shown the behaviour of average relative power during 6 second.
Fig. 1. Behavior of average power during the transient.
Table 1 presents performance results shown by the parallel code on the distributed-memory multicomputer MBC-100 [10] based on i860-XP processors. In this problem grid points were distributed over processors in Z and Y directions (denoted by 4*8 meaning 32 processor grid of 4 rows and 8 columns in Z and Y directions correspondingly, arrays were divided into 4 equal portions over Z-axis and approximately into 8 equal portions over Y-axis).
Table 1. Parallel efficiency of Fortran-DVM code.
N |
1*1 |
1*2 |
2*2 |
2*5 |
5*2 |
4*4 |
11*2 |
4*8 |
8*8 |
E |
100% |
97% |
97% |
69% |
83% |
65% |
99% |
48% |
37% |
In this Table E means the parallelization
efficiency: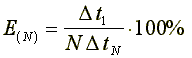 
,
where 
stands for the time
shown by the single processor code and 
is the time reported by
the N processor code.
ACKNOWLEDGEMENTS
This research was performed under the financial support of ISTC Project # 115-95, Project RFFI # 97-01-00390 and Project INTAS-RFBR # 95-0369.
REFERENCES
